Suppose you want to study a structural VAR model under the common trends model hypothesis; (see King, Plosser, Stock and Watson (1991) and see Warne (1993)). Suppose further that the VAR system consists of 5 endogenous variables with 2 cointegration relations. In this case we need to impose 10 restrictions (in addition to the 15 restrictions imposed on the covariance matrix of the structural shocks).
Let A=C*B be the long-run responses from the structural shocks. Here, the matrix C has rank equal to 3 and contains the parameters on the accumulated reduced-form residuals (see Johansen (1996)), while B has rank 5 and represents to contemporaneous effects on the endogenous variables from the shocks. Suppose further that the 3 permanent or trend shocks are grouped first while the 2 transitory shocks are grouped last. In addition, suppose we want to obtain an A matrix of the form (where * indicates any real number):
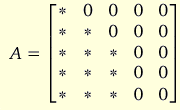
This matrix has 13 zeros and it cannot identify the last 2 shocks since their long-run effects are the same. The first 3 shocks, however, can be identified since they have different long-run effects on the first 3 variables. If you tell SVAR to use these 13 zero restrictions as part of the identification scheme, it will complain that some of the restrictions are linearly dependent and refuse to estimate the structural form. Below we will discuss how to impose the 13 zeros and how many restrictions you need to include to obtain them.
Suppose we impose the following 7 restrictions on the A matrix:
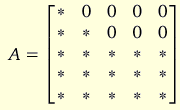
The rank of this matrix must be 3. Since SVAR will make the upper left 2x2 part of this matrix of full rank when the first 2 variables are restricted to be I(1), it follows that the last 3 columns will be linearly dependent and of rank 1. To ensure that the bottom right 3x2 matrix here has zeros we need to impose 2 additional restrictions on A.
The fact that the rank of the bottom right 3x3 matrix in A is 1 means that we can express this part as
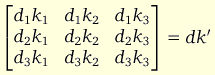
where d and k are non-zero vectors. Suppose a is non-zero. This implies that the 3rd endogenous variable is non-stationary (if it were stationary the whole 3rd row of C and A would be zero). From this we can see that if we let elements (3,4) and (3,5) be 0 in the A matrix all elements in the 4th and 5th column of A will be zero as well. That is, we effectively set k2 = k3 = 0. Hence, by choosing the following form for the A matrix:
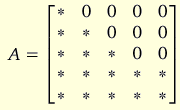
the rank 3 requirement means that the lower right 2x2 matrix is zero as well. Hence, the number of identifying restrictions imposed on A is 9. To achieve exact identification we need to impose 1 restriction on B which separates the contemporaneous effects of the transitory shocks. One such case would be to let B(5,4)=0.


